Zadanie nr 5344709
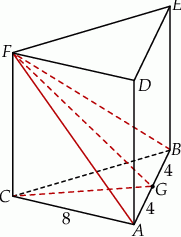
Dany jest graniastosłup prawidłowy trójkątny 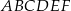 o podstawach
o podstawach 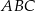 i
i 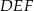 i krawędziach bocznych
i krawędziach bocznych 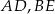 i
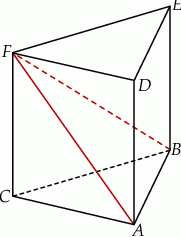
i 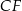 (zobacz rysunek). Długość krawędzi podstawy
(zobacz rysunek). Długość krawędzi podstawy 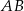 jest równa 8, a pole trójkąta
jest równa 8, a pole trójkąta 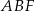 jest równe 52. Oblicz objętość tego graniastosłupa.
jest równe 52. Oblicz objętość tego graniastosłupa.
Rozwiązanie
Zauważmy, że trójkąt 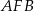 jest równoramienny więc jego wysokość
jest równoramienny więc jego wysokość 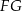 opuszczona z wierzchołka
opuszczona z wierzchołka 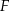 dzieli krawędź
dzieli krawędź 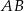 na połowy.
na połowy.
Z podanego pola trójkąta 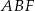 możemy obliczyć długość odcinka
możemy obliczyć długość odcinka 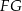 .
.
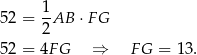
Sposób I
Odcinek 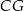 to wysokość trójkąta równobocznego w podstawie graniastosłupa, czyli
to wysokość trójkąta równobocznego w podstawie graniastosłupa, czyli
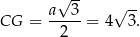
Piszemy teraz twierdzenie Pitagorasa w trójkącie 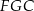 .
.
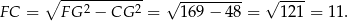
Pozostało obliczyć objętość graniastosłupa.
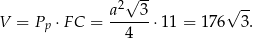
Sposób II
Stosujemy twierdzenie Pitagorasa w trójkącie 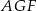 .
.
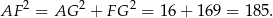
Teraz patrzymy na trójkąt prostokątny 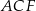 .
.
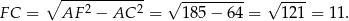
Pozostało obliczyć objętość graniastosłupa.
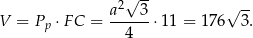
Odpowiedź: