/Szkoła średnia/Geometria/Stereometria

Zadanie nr 5355228

Dodaj do ulubionych
Dodaj do rozwiązanych

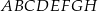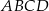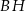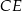Podstawą prostopadłościanu ABCDEF GH o wysokości 4 jest kwadrat ABCD o boku 3. Oblicz sinus kąta, pod którym przecinają się przekątne BH i CE tego prostopadłościanu.

Rozwiązanie

Szkicujemy prostopadłościan.

PIC

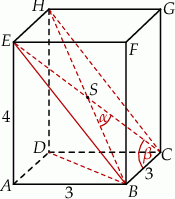
Korzystamy z twierdzenia Pitagorasa i obliczamy długość przekątnej ściany i długość przekątnej prostopadłościanu.

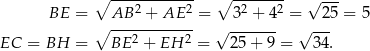
∘ ------------ ∘ ------- √ --- BE = AB 2 + AE 2 = 32 + 42 = 25 = 5 ∘ ------------ √ ------- √ --- EC = BH = BE 2 + EH 2 = 25 + 9 = 34.

Sposób I

Skorzystamy z twierdzenia sinusów w trójkącie 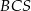BCS . Zanim jednak to zrobimy obliczamy sin β .

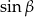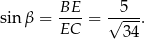
BE 5 sinβ = ----= √---. EC 34

Zapisujemy teraz twierdzenie sinusów.

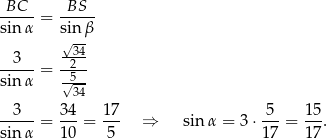
BC---= -BS-- sin α sin β √-34- -3---= -2-- sin α √5-- 34 -3---= 34-= 17- ⇒ sin α = 3⋅ 5--= 1-5. sin α 10 5 17 1 7

Sposób II

Interesujący nas sinus kąta między przekątnymi możemy obliczyć korzystając ze wzoru na pole trójkąta z sinusem.

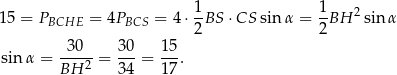
1 1 2 15 = PBCHE = 4PBCS = 4 ⋅--BS ⋅CS sin α = -BH sin α 2 2 sinα = -30--= 30-= 15. BH 2 34 17

Sposób III

Tym razem skorzystamy z tego, że

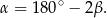
α = 180∘ − 2β .

Mamy zatem

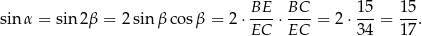
BE BC 15 15 sinα = sin 2β = 2sin βco sβ = 2 ⋅----⋅ ----= 2 ⋅---= --. EC EC 34 17

 
Odpowiedź: 15 17

Wersja PDF