Zadanie nr 5393112
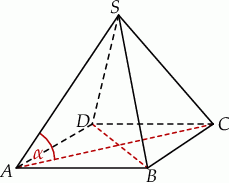
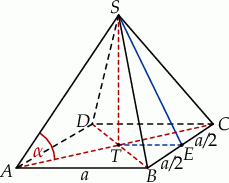
Kąt  jest kątem nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy (zobacz rysunek). Oblicz stosunek pola powierzchni całkowitej tego ostrosłupa do pola jego podstawy, jeżeli
jest kątem nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy (zobacz rysunek). Oblicz stosunek pola powierzchni całkowitej tego ostrosłupa do pola jego podstawy, jeżeli 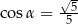 .
.
Rozwiązanie
Dorysujmy wysokość 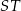 ostrosłupa oraz wysokość
ostrosłupa oraz wysokość 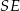 jego ściany bocznej. Oznaczmy też przez
jego ściany bocznej. Oznaczmy też przez  długość krawędzi podstawy ostrosłupa.
długość krawędzi podstawy ostrosłupa.
Z podanego 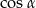 obliczamy długość krawędzi bocznej ostrosłupa
obliczamy długość krawędzi bocznej ostrosłupa
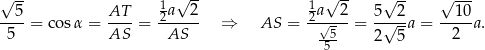
Obliczamy teraz z trójkąta prostokątnego 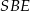 długość wysokości ściany bocznej
długość wysokości ściany bocznej
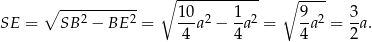
Teraz łatwo już obliczyć interesujący nas stosunek pola powierzchni całkowitej do pola podstawy
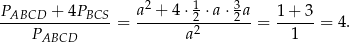
Odpowiedź: