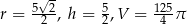/Szkoła średnia/Geometria/Stereometria

Zadanie nr 5611662

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozpatrujemy wszystkie walce, których przekrojem osiowym jest prostokąt, w którym suma długości przekątnej i jednego boku jest równa 10. Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz objętość tego walca.

Rozwiązanie

Szkicujemy walec

PIC

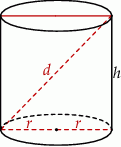
Zauważmy, że z podanych informacji nie wynika, który bok prostokąta bierzemy pod uwagę, więc rozważymy dwie sytuacje.

Przyjmijmy najpierw, że 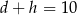d+ h = 10 i za parametr przyjmijmy 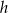h . Mamy wtedy

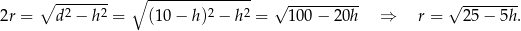
--------------- ∘ -2----2- ∘ 2 2 √ ---------- √ -------- 2r = d − h = (10 − h ) − h = 100 − 20h ⇒ r = 25 − 5h.

Objętość walca jest więc równa

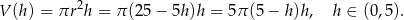
2 V (h) = πr h = π (25 − 5h)h = 5π(5 − h )h, h ∈ (0,5).

Wykresem tej funkcji jest parabola o ramionach skierowanych w dół, więc wartość największą objętości otrzymamy dla 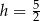h = 52 (dokładnie w połowie między pierwiastkami). Promień podstawy walca jest wtedy równy

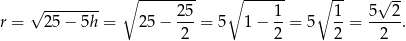
∘ -------- ∘ ------ ∘ -- √ -- √ -------- 2 5 1 1 5 2 r = 25 − 5h = 25 − --- = 5 1− --= 5 --= ----. 2 2 2 2

Objętość jest wtedy równa

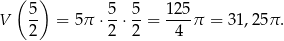
( 5 ) 5 5 1 25 V -- = 5π ⋅--⋅ --= ----π = 31,25π . 2 2 2 4

Teraz zajmijmy się drugą sytuacją, gdy 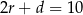2r+ d = 10 . Tym razem za parametr przyjmijmy r . Mamy wtedy

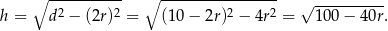
∘ ---------- ∘ ---------------- h = d2 − (2r)2 = (1 0− 2r)2 − 4r2 = √ 100−--40r.

Objętość walca jest równa

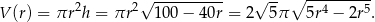
2 2√ ---------- √ -- ∘ --------- V (r) = πr h = πr 1 00− 40r = 2 5π 5r 4 − 2r5.

Wyznaczenie największej wartości objętości sprowadza się więc do wyznaczenia największej wartości funkcji

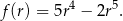
f(r) = 5r4 − 2r5.

Dziedziną tej funkcji jest przedział 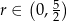r ∈ (0, 5) 2 (bo musi być 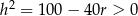h2 = 100 − 4 0r > 0 ). Liczymy pochodną

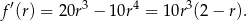
′ 3 4 3 f (r) = 20r − 10r = 10r (2− r).

Widać teraz, że pochodna jest dodatnia w przedziale 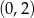(0,2) i ujemna w przedziale 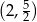( 5) 2,2 . To oznacza, że funkcja 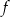f rośnie w przedziale 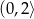(0,2⟩ i maleje w przedziale 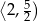⟨ 5) 2,2 . W takim razie największą wartość objętość otrzymamy dla r = 2 .

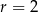Wysokość dla 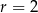r = 2 jest równa

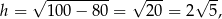
√ --------- √ --- √ -- h = 100 − 8 0 = 20 = 2 5,

a objętość wynosi

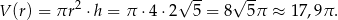
√ -- √ -- V(r) = πr 2 ⋅ h = π ⋅4 ⋅2 5 = 8 5π ≈ 17,9π .

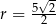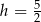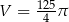Objętość ta jest mniejsza niż w pierwszym przypadku, więc walcem o największej objętości jest walec o promieniu podstawy - 5√-2 r = 2 , wysokości h = 52 i objętości V = 1254 π .  
Odpowiedź: √ - r = 5-2, h = 5,V = 125π 2 2 4

Wersja PDF