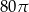/Szkoła średnia/Geometria/Stereometria

Zadanie nr 5632337

Dodaj do ulubionych
Dodaj do rozwiązanych

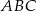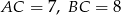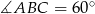W trójkącie ostrokątnym ABC mamy AC = 7, BC = 8 , zaś ∘ ∡ABC = 60 . Oblicz objętość bryły powstałej z obrotu trójkąta 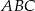ABC wokół prostej zawierającej bok AB .

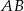Rozwiązanie

Zaczynamy od rysunku.

PIC

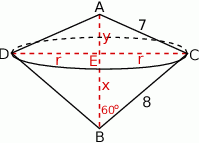
Powstałą bryłę możemy podzielić na dwa stożki, które w podstawie mają koło o promieniu 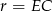r = EC . Zarówno ten promień, jak i wysokość x dolnego stożka wyliczamy z trójkąta BCE .

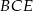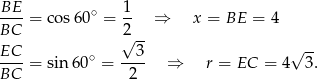
BE-- ∘ 1- BC = cos6 0 = 2 ⇒ x = BE = 4 √ -- √ -- EC--= sin60 ∘ = --3- ⇒ r = EC = 4 3. BC 2

Obliczmy jeszcze wysokość 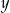y górnego stożka.

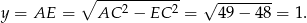
∘ ------------ √ -------- y = AE = AC 2 − EC 2 = 49− 48 = 1.

Możemy teraz obliczyć objętość powstałej bryły.

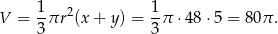
V = 1πr 2(x + y) = 1π ⋅48 ⋅5 = 80π. 3 3

 
Odpowiedź: 80π

Wersja PDF