Zadanie nr 5639561
Krawędź podstawy ostrosłupa prawidłowego czworokątnego 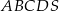 ma długość
ma długość  . Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem
. Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 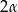 . Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.
. Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.
Rozwiązanie
Szkicujemy opisaną sytuację.
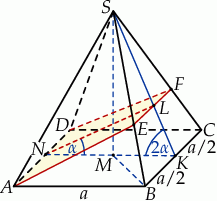
Otrzymany przekrój 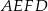 jest trapezem równoramiennym, więc do obliczenia jego pola potrzebujemy obliczyć długości podstaw i wysokość. Jedną podstawę znamy
jest trapezem równoramiennym, więc do obliczenia jego pola potrzebujemy obliczyć długości podstaw i wysokość. Jedną podstawę znamy 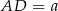 , a wysokość łatwo obliczyć z trójkąta
, a wysokość łatwo obliczyć z trójkąta 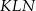 . Piszemy twierdzenie sinusów w tym trójkącie.
. Piszemy twierdzenie sinusów w tym trójkącie.
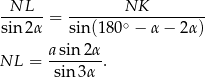
Pozostało zająć się drugą podstawą trapezu. Spróbujemy ją obliczyć z trójkąta 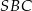 , ale najpierw obliczmy długości odcinków
, ale najpierw obliczmy długości odcinków 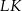 i
i 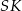 . Odcinek
. Odcinek 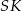 obliczamy z trójkąta prostokątnego
obliczamy z trójkąta prostokątnego 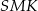 .
.
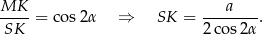
Odcinek 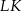 obliczamy ponownie stosując twierdzenie sinusów w trójkącie
obliczamy ponownie stosując twierdzenie sinusów w trójkącie 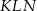 .
.
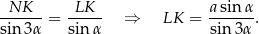
Teraz obliczamy długość drugiej podstawy – korzystamy z podobieństwa trójkątów 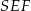 i
i 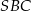 .
.
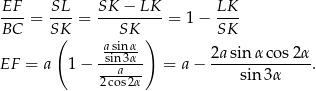
Pozostało obliczyć pole przekroju.
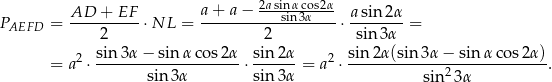
Odpowiedź: