/Szkoła średnia/Geometria/Stereometria

Zadanie nr 5887735

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 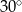30 ∘ . Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.

Rozwiązanie

Oznaczmy przez a długość krawędzi podstawy ostrosłupa.

PIC

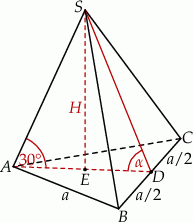
Wiemy, że

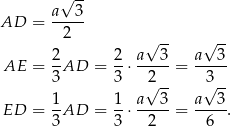
√ -- AD = a--3- 2 2 2 a√ 3- a√ 3- AE = --AD = -⋅ -----= ----- 3 3 2√ -- 3√ -- 1- 1- a--3- a--3- ED = 3 AD = 3 ⋅ 2 = 6 .

Wiemy ponadto, że

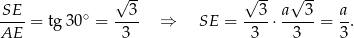
√ -- √ -- √ -- SE ∘ 3 3 a 3 a ----= tg 30 = ---- ⇒ SE = ----⋅ -----= -. AE 3 3 3 3

Stąd

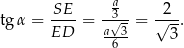
SE a3 2 tg α = ED-- = -a√-3 = √--. -6-- 3

Pozostało obliczyć cosinus

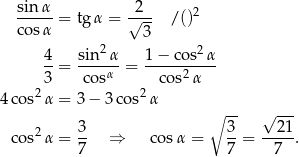
sin α 2 -----= tgα = √--- /()2 cosα 3 4 sin2α 1 − co s2 α --= ----α- = ------2--- 23 cos 2 co s α 4 cos α = 3− 3co s α 3 ∘ -3 √ 2-1 cos2α = -- ⇒ cos α = --= -----. 7 7 7

 
Odpowiedź: √ -- --271

Wersja PDF