/Szkoła średnia/Geometria/Stereometria

Zadanie nr 6031616

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości krawędzi podstawy prostopadłościanu są równe 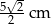5√2- 2 cm , a krawędź boczna ma długość 2 cm. Oblicz pole przekroju tego graniastosłupa płaszczyzną zawierającą przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem 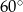60 ∘ . Sporządź rysunek i zaznacz na nim przekrój oraz kąt jego nachylenia do płaszczyzny podstawy.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

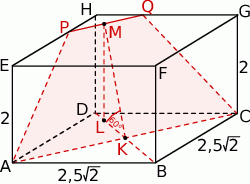
W przekroju otrzymujemy trapez równoramienny, którego dłuższa podstawa ma długość

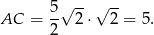
√ --√ -- AC = 5- 2⋅ 2 = 5. 2

Łatwo też obliczyć wysokość tego trapezu – patrzymy na trójkąt prostokątny 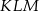KLM (punkt 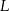L jest rzutem środka podstawy 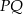PQ trapezu).

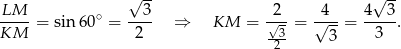
√ -- √ -- LM-- ∘ --3- -2- -4-- 4---3 KM = sin6 0 = 2 ⇒ KM = √-3 = √ 3-= 3 . 2

Ponadto

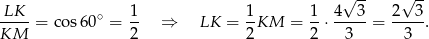
√ -- √ -- LK-- = cos 60∘ = 1- ⇒ LK = 1-KM = 1-⋅ 4--3 = 2--3-. KM 2 2 2 3 3

Patrzymy teraz na równoramienny trójkąt prostokątny 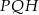PQH – jest to połówka kwadratu, więc

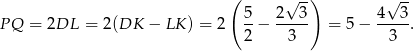
( √ -) √ -- PQ = 2DL = 2(DK − LK ) = 2 5-− 2---3 = 5 − 4--3-. 2 3 3

Pole przekroju jest więc równe

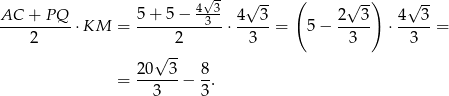
√ - 4--3 √ -- ( √ -) √ -- AC--+--PQ- ⋅KM = 5-+-5-−--3--⋅ 4--3-= 5 − 2---3 ⋅ 4--3-= 2 2 3 3 3 √ -- = 20--3-− 8. 3 3

 
Odpowiedź: 20√-3−-8 2 3 cm

Wersja PDF