Zadanie nr 6097739
Środki ścian czworościanu foremnego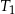 
są wierzchołkami czworościanu 
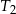. Oblicz stosunek objętości czworościanów 
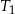i 
.
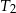Rozwiązanie
Szkicujemy czworościan foremny.
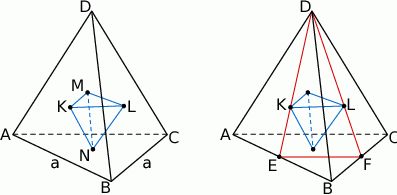
Obliczymy długość jednej z krawędzi, powiedzmy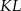 
, mniejszego czworościanu 
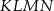w zależności od długości 
krawędzi dużego czworościanu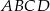 
. Punkty 
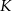i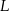 
leżą na wysokościach 
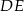i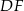 
trójkątów równobocznych 
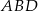i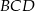 
i dzielą je w stosunku 2:1 (licząc od wierzchołka 
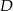). To oznacza, że trójkąty 
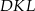i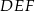 
są podobne w skali 2:3. W szczególności
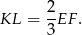
Odcinek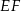 
to odcinek łączący środki boków w trójkącie 
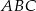, więc
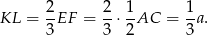
Oczywiście dokładnie w ten sam sposób możemy obliczyć długości pozostałych krawędzi czworościanu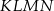 
, więc czworościan ten też jest czworościanem foremnym, ale 3 razy mniejszym od czworościanu 
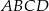. W takim razie jego objętość jest 
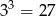razy mniejsza od objętości czworościanu 
.
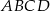Odpowiedź: 
