Zadanie nr 6098664
Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy 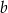 i kącie nachylenia krawędzi bocznej do krawędzi podstawy
i kącie nachylenia krawędzi bocznej do krawędzi podstawy  . Oblicz pole przekroju płaszczyzną przechodzącą przez wierzchołek i równoległą do krawędzi podstawy oraz nachyloną do płaszczyzny podstawy pod kątem
. Oblicz pole przekroju płaszczyzną przechodzącą przez wierzchołek i równoległą do krawędzi podstawy oraz nachyloną do płaszczyzny podstawy pod kątem 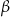 . Podaj konieczne założenia dotyczące kąta
. Podaj konieczne założenia dotyczące kąta  .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
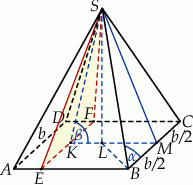
Przekrój 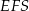 , o którym mowa w treści zadania to trójkąt równoramienny o podstawie
, o którym mowa w treści zadania to trójkąt równoramienny o podstawie 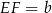 i wysokości
i wysokości 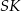 . Tę wysokość łatwo powiązać z wysokością ostrosłupa – patrzymy na trójkąt prostokątny
. Tę wysokość łatwo powiązać z wysokością ostrosłupa – patrzymy na trójkąt prostokątny 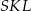
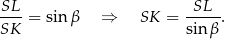
Pole trójkąta 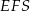 jest więc równe
jest więc równe
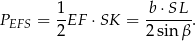
Pozostało więc obliczyć wysokość ostrosłupa 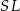 – zrobimy to na dwa sposoby. Zanim jednak przejdziemy do tych rachunków, ustalmy jeszcze jakie są możliwe wartość kąta
– zrobimy to na dwa sposoby. Zanim jednak przejdziemy do tych rachunków, ustalmy jeszcze jakie są możliwe wartość kąta  . Jeżeli odsuwamy wierzchołek
. Jeżeli odsuwamy wierzchołek 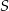 od płaszczyzny podstawy, to kąt ten rośnie i może być dowolnie bliski
od płaszczyzny podstawy, to kąt ten rośnie i może być dowolnie bliski 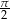 , a jeżeli przybliżamy wierzchołek
, a jeżeli przybliżamy wierzchołek 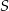 do płaszczyzny podstawy, to trójkąt
do płaszczyzny podstawy, to trójkąt 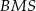 zaczyna przybliżać trójkąt
zaczyna przybliżać trójkąt 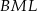 i kąt ten dąży do
i kąt ten dąży do 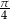 . Zatem
. Zatem
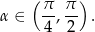
Gdybyśmy chcieli tę samą odpowiedź otrzymać bardziej rachunkowo, niż geometrycznie, to patrzymy na trójkąt 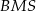 , w którym
, w którym 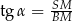 i zauważamy, że
i zauważamy, że 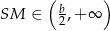 .
.
Sposób I
Wysokość ostrosłupa obliczymy z trójkąta prostokątnego 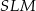 . Najpierw jednak obliczamy długość wysokości
. Najpierw jednak obliczamy długość wysokości 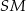 ściany bocznej.
ściany bocznej.
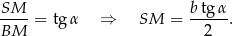
Piszemy teraz twierdzenie Pitagorasa w trójkącie 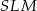 .
.
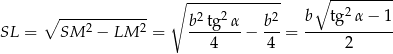
Pole przekroju jest więc równe
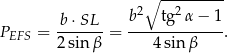
Sposób II
Tym razem wysokość ostrosłupa obliczymy z trójkąta prostokątnego 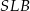 . Najpierw obliczamy jednak długość krawędzi bocznej ostrosłupa.
. Najpierw obliczamy jednak długość krawędzi bocznej ostrosłupa.
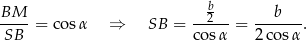
Piszemy teraz twierdzenie Pitagorasa w trójkącie 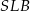 .
.
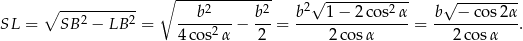
Pole przekroju jest więc równe
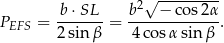
Odpowiedź: 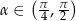 ,
,