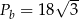/Szkoła średnia/Geometria/Stereometria

Zadanie nr 6234659

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ostrosłup prawidłowy trójkątny. Promień okręgu opisanego na podstawie tego ostrosłupa jest równy 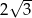√ -- 2 3 . Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 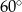60∘ . Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku

PIC

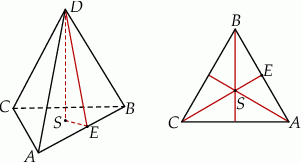
Promień okręgu opisanego na trójkącie równobocznym stanowi 23 wysokości tego trójkąta. Zatem

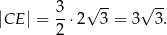
√ -- √ -- |CE | = 3-⋅2 3 = 3 3. 2

Ze wzoru na długość wysokości trójkąta równobocznego wyznaczamy długość boku

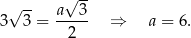
√ -- √ -- a---3 3 3 = 2 ⇒ a = 6 .

Ponieważ odcinek 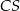CS jest promieniem okręgu opisanego, więc

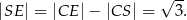
√ -- |SE| = |CE |− |CS | = 3.

Korzystamy z tego, że 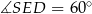∡SED = 6 0∘ i obliczamy wysokość ostrosłupa

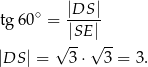
∘ |DS-| tg6 0 = |SE | √ -- √ -- |DS | = 3 ⋅ 3 = 3.

Obliczamy pole podstawy

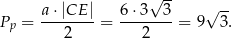
√ -- -- P = a⋅|CE-|-= 6⋅3---3-= 9√ 3. p 2 2

Teraz już łatwo obliczyć objętość

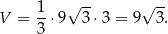
√ -- √ -- V = 1-⋅9 3⋅3 = 9 3. 3

Z twierdzenia Pitagorasa obliczamy wysokość ściany bocznej

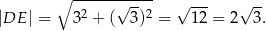
∘ ------√---- √ --- √ -- |DE | = 32 + ( 3)2 = 12 = 2 3.

Liczymy pole ściany bocznej

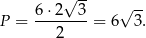
√ -- 6⋅2 3 √ -- P = --------= 6 3 . 2

Zatem pole boczne wynosi

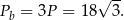
P = 3P = 18√ 3. b

 
Odpowiedź: 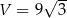√ -- V = 9 3 i √ -- Pb = 18 3

Wersja PDF