Zadanie nr 6464491
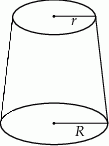
Przedstawiona na rysunku bryła to stożek ścięty płaszczyzną równoległą do jego płaszczyzny podstawy. Wysokość tej bryły jest równa 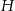 , a
, a  i
i 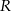 (
(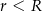 ) są promieniami podstaw. Oblicz objętość tej bryły.
) są promieniami podstaw. Oblicz objętość tej bryły.
Rozwiązanie
Dorysujmy brakującą część stożka.
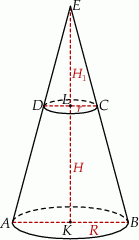
Jeżeli 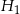 jest wysokością odciętego stożka, to z podobieństwa trójkątów
jest wysokością odciętego stożka, to z podobieństwa trójkątów 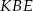 i
i 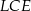 mamy
mamy
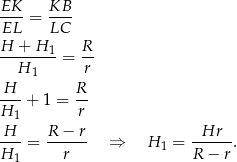
Liczymy teraz objętość ściętego stożka
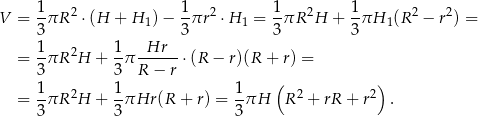
Odpowiedź: