Zadanie nr 6519144
Oblicz objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 4 dm i krawędzi bocznej 6 dm.
Rozwiązanie
Zaczynamy od schematycznego rysunku.
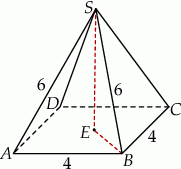
Zacznijmy od obliczenia wysokości 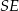 ostrosłupa. Odcinek
ostrosłupa. Odcinek 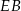 jest równy połowie długości przekątnej podstawy, czyli ma długość
jest równy połowie długości przekątnej podstawy, czyli ma długość 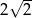 . Stosujemy twierdzenie Pitagorasa w trójkącie prostokątnym
. Stosujemy twierdzenie Pitagorasa w trójkącie prostokątnym 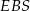 .
.
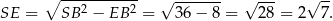
Zatem objętość jest równa
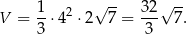
Odpowiedź: