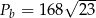Zadanie nr 6558564
Dany jest ostrosłup prawidłowy czworokątny o wysokości 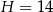 . Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
. Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy  . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Rozwiązanie
Rozpoczynamy od rysunku.
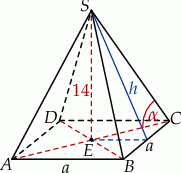
Oznaczmy przez  długość krawędzi podstawy graniastosłupa. Korzystając ze wzoru na długość przekątnej kwadratu mamy
długość krawędzi podstawy graniastosłupa. Korzystając ze wzoru na długość przekątnej kwadratu mamy
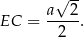
Z podanego cosinusa kąta  między krawędzią ostrosłupa, a płaszczyzną podstawy mamy
między krawędzią ostrosłupa, a płaszczyzną podstawy mamy
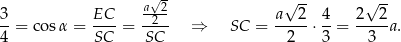
Piszemy teraz twierdzenie Pitagorasa w trójkącie prostokątnym 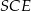 .
.
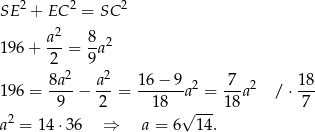
Obliczamy jeszcze wysokość 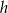 ściany bocznej ostrosłupa.
ściany bocznej ostrosłupa.
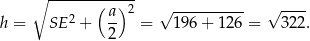
Pozostało obliczyć pole powierzchni bocznej ostrosłupa.
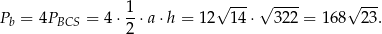
Odpowiedź: