/Szkoła średnia/Geometria/Stereometria

Zadanie nr 6674603

Dodaj do ulubionych
Dodaj do rozwiązanych

Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 4 cm i jest nachylona do płaszczyzny podstawy pod kątem 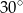30∘ . Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku.

PIC

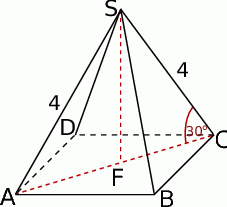
Z trójkąta prostokątnego 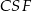CSF wyliczamy wysokość i połowę przekątnej podstawy czworościanu.

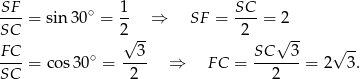
SF-= sin 30∘ = 1- ⇒ SF = SC-= 2 SC 2 2 FC √ 3- SC √ 3- √ -- ---= cos 30∘ = ---- ⇒ FC = -------= 2 3. SC 2 2

Ponieważ 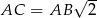√ -- AC = AB 2 mamy

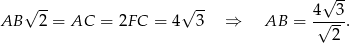
√ -- √ -- 4√ 3- AB 2 = AC = 2F C = 4 3 ⇒ AB = √---. 2

Zatem pole podstawy jest równe

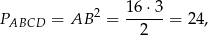
PABCD = AB 2 = 16-⋅3-= 2 4, 2

a objętość

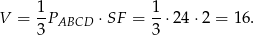
1 1 V = -PABCD ⋅SF = --⋅24 ⋅2 = 16. 3 3

Ponieważ objętość sześcianu o krawędzi długości a jest równa 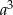3 a , szukana krawędź sześcianu spełnia

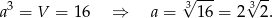
√ --- √ -- a3 = V = 1 6 ⇒ a = 316 = 2 32.

 
Odpowiedź: √ -- 2 32 cm

Wersja PDF