/Szkoła średnia/Geometria/Stereometria

Zadanie nr 6765703

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest stożek o objętości 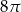8π , w którym stosunek wysokości do promienia podstawy jest równy 3:8. Oblicz pole powierzchni bocznej tego stożka.

Rozwiązanie

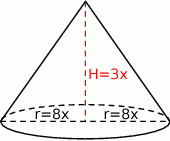
Niech 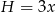H = 3x będzie wysokością, a 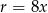r = 8x promieniem podstawy stożka.

PIC

Wykorzystujemy informację o objętości, aby obliczyć x .

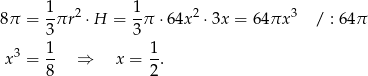
8π = 1πr 2 ⋅ H = 1π ⋅ 64x2 ⋅3x = 64 πx 3 / : 64π 3 3 3 1- 1- x = 8 ⇒ x = 2 .

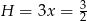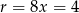Mamy zatem H = 3x = 32 i r = 8x = 4 . Obliczamy jeszcze długość 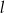l tworzącej stożka

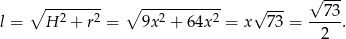
√ --- ∘ -------- ∘ ----------- √ --- 73 l = H 2 + r2 = 9x2 + 64x2 = x 73 = ----. 2

Pole powierzchni bocznej stożka jest więc równe

√ --- 7 3 √ --- Pb = πrl = π ⋅4 ⋅----- = 2 73 π. 2

 
Odpowiedź: √ --- 2 73 π

Wersja PDF