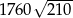Zadanie nr 6879292
Podstawą ostrosłupa 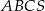 jest trójkąt równoramienny
jest trójkąt równoramienny 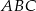 . Krawędź
. Krawędź 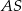 jest wysokością ostrosłupa oraz
jest wysokością ostrosłupa oraz 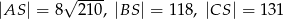 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Najtrudniejsza część tego zadania to ustalenie, które boki trójkąta 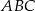 są równe.
są równe.
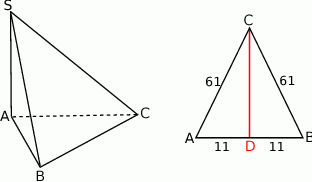
Gdy naszkicujemy ostrosłup, w którym 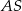 jest wysokością, to widać, że trójkąty
jest wysokością, to widać, że trójkąty 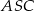 i
i 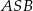 są prostokątne. To pozwala łatwo obliczyć długości krawędzi
są prostokątne. To pozwala łatwo obliczyć długości krawędzi 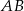 i
i 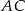 .
.
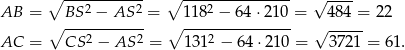
W takim razie 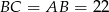 lub
lub 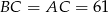 . Pierwszy przypadek jest jednak niemożliwy, bo
. Pierwszy przypadek jest jednak niemożliwy, bo 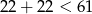 . Zatem
. Zatem 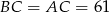 .
.
Aby obliczyć objętość ostrosłupa, potrzebujemy obliczyć pole jego podstawy. Można to zrobić ze wzoru Herona, ale my zrobimy to bardziej elementarnie. Dorysujmy wysokość 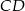 trójkąta
trójkąta 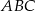 . Ponieważ trójkąt
. Ponieważ trójkąt 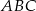 jest równoramienny, punkt
jest równoramienny, punkt 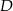 jest środkiem odcinka
jest środkiem odcinka 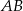 i mamy
i mamy
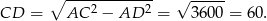
Zatem
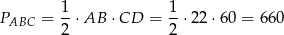
i objętość ostrosłupa jest równa
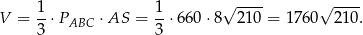
Odpowiedź: