Zadanie nr 6931920
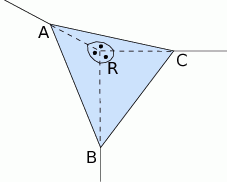
Narożnik między dwiema ścianami i sufitem prostopadłościennego pokoju należy zamaskować trójkątnym fragmentem płyty gipsowo-kartonowej (patrz rysunek). Wiedząc, że 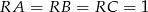 m, oblicz objętość narożnika zamaskowanego tą płytą. Wynik zaokrąglij do 0,01
m, oblicz objętość narożnika zamaskowanego tą płytą. Wynik zaokrąglij do 0,01 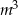 .
.
Rozwiązanie
Opisany narożnik możemy traktować jak ostrosłup o podstawie 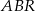 i wysokości
i wysokości 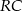 . Ponieważ pole
. Ponieważ pole 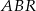 jest równe
jest równe 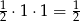 oraz
oraz 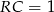 , szukana objętość wynosi
, szukana objętość wynosi
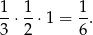
Ponieważ 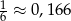 , to po zaokrągleniu mamy
, to po zaokrągleniu mamy 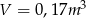 .
.
Odpowiedź: