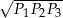Zadanie nr 6961299
W prostopadłościanie pola trzech ścian o wspólnym wierzchołku są równe 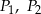 i
i 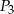 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Rozwiązanie
Zacznijmy od obrazka.
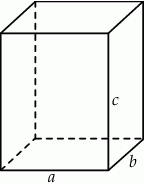
Oznaczmy krawędzie prostopadłościanu przez 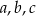 tak aby
tak aby
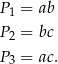
Mnożymy te równości stronami i mamy
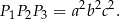
Zatem objętość prostopadłościanu jest równa
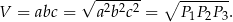
Odpowiedź: