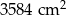/Szkoła średnia/Geometria/Stereometria

Zadanie nr 7106025

Dodaj do ulubionych
Dodaj do rozwiązanych

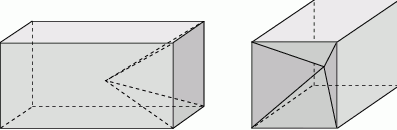
Z drewnianego prostopadłościanu o objętości 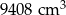3 940 8 cm i podstawie będącej kwadratem o boku 14 cm, wycięto ostrosłup prawidłowy czworokątny o wysokości równej połowie najdłuższej krawędzi prostopadłościanu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Oblicz pole powierzchni całkowitej otrzymanej bryły.

PIC

Rozwiązanie

Z podanej objętości prostopadłościanu obliczamy długość x jego trzeciej krawędzi.

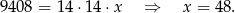
9408 = 14⋅1 4⋅x ⇒ x = 48 .

Powierzchnia otrzymanej bryły składa się z kwadratu, czterech prostokątów oraz czterech trójkątów. Z powierzchnią kwadratu i prostokątów nie ma problemu:

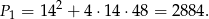
P1 = 142 + 4 ⋅14 ⋅48 = 288 4.

Odrobinę bardziej musimy się wysilić z trójkątami, bo nie znamy ich wysokości 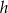h . Aby ją obliczyć narysujmy wycięty ostrosłup.

PIC

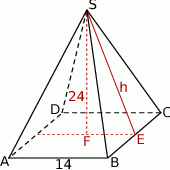
Widać teraz, że wysokość 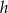h interesujących nas trójkątów możemy obliczyć z twierdzenia Pitagorasa w trójkącie prostokątnym SF E .

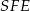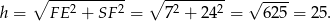
∘ ----------- ∘ --------- √ ---- h = FE 2 + SF2 = 72 + 242 = 625 = 25.

Teraz bez problemu obliczamy pole powierzchni trzech ścian bocznych wyciętego ostrosłupa.

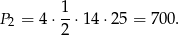
1- P2 = 4 ⋅2 ⋅14 ⋅25 = 70 0.

Pole powierzchni całkowitej otrzymanej bryły jest więc równe

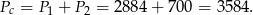
Pc = P1 + P2 = 28 84+ 700 = 35 84.

 
Odpowiedź: 358 4 cm 2

Wersja PDF