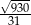/Szkoła średnia/Geometria/Stereometria

Zadanie nr 7125548

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ostrosłup prawidłowy czworokątny 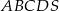ABCDS o podstawie 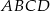ABCD . Ramię trójkąta równoramiennego 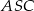ASC ma długość 8 i jest dwa razy dłuższe od jego podstawy. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.

PIC

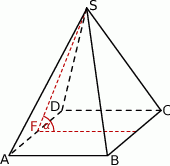
Rozwiązanie

Dorysujmy przekątną podstawy ostrosłupa oraz jego wysokość.

PIC

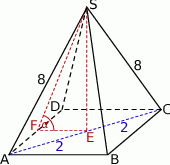
Z trójkąta prostokątnego 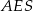AES obliczamy długość wysokości ostrosłupa.

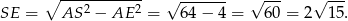
∘ ------------ √ ------- √ --- √ --- SE = AS 2 − AE 2 = 64 − 4 = 60 = 2 15.

Znamy długość przekątnej kwadratu ABCD , więc możemy obliczyć długość jego boku.

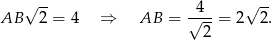
-- -- AB √ 2 = 4 ⇒ AB = √4--= 2√ 2. 2

Z trójkąta prostokątnego SF E obliczamy długość odcinka FS .

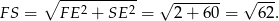
∘ ----------- √ ------- √ --- FS = F E2 + SE 2 = 2+ 60 = 62.

Mamy więc

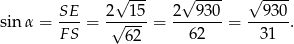
√ --- √ ---- √ ---- SE 2 15 2 930 930 sinα = FS- = -√---- = ---62-- = -31--. 62

 
Odpowiedź: √ 930 --31--

Wersja PDF