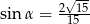Zadanie nr 7150064
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest dwa razy dłuższa od krawędzi podstawy. Krawędź podstawy jest równa  . Oblicz pole powierzchni bocznej i sinus połowy kąta między ścianami bocznymi ostrosłupa.
. Oblicz pole powierzchni bocznej i sinus połowy kąta między ścianami bocznymi ostrosłupa.
Rozwiązanie
Zaczynamy od rysunku
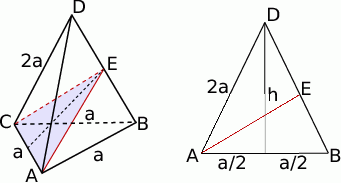
Najpierw policzymy pole powierzchni bocznej. Ponieważ wszystkie trzy ściany boczne są identyczne, więc wystarczy policzyć pole jednej z nich np. 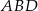 . Obliczamy wysokość
. Obliczamy wysokość
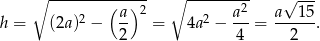
Zatem pole boczne wynosi
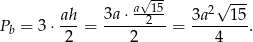
Teraz zajmiemy się kątem między ścianami bocznymi – jest to dokładnie kąt między wysokościami 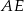 i
i 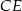 trójkątów
trójkątów 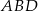 i
i 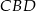 . Wysokości te mają równe długości – wyliczymy je licząc na dwa sposoby pole trójkąta
. Wysokości te mają równe długości – wyliczymy je licząc na dwa sposoby pole trójkąta 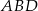 .
.
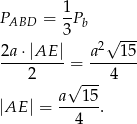
Zatem trójkąt 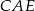 wygląda następująco
wygląda następująco
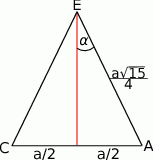
Widać, że  jest połową kąta między ścianami. Zatem
jest połową kąta między ścianami. Zatem
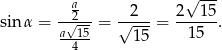
Odpowiedź: 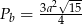 i
i