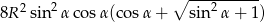Zadanie nr 7228501
Krawędź boczna ostrosłupa prawidłowego czworokątnego wpisanego w kulę o promieniu 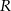 tworzy z płaszczyzną podstawy kąt
tworzy z płaszczyzną podstawy kąt  . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
Rozwiązanie
Zaczynamy od rysunku.
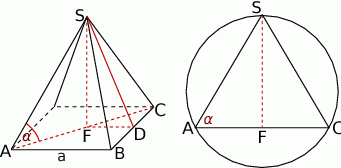
Podana informacja o promeniu kuli opisanej na ostrosłupie, mówi nam w szczególności, że promień okręgu opisanego na trójkącie 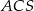 jest równy
jest równy 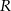 . To pozwala (z twierdzenia sinusów) łatwo wyliczyć krawędź boczną.
. To pozwala (z twierdzenia sinusów) łatwo wyliczyć krawędź boczną.
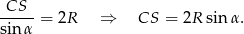
Teraz, z trójkąta 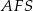 wyliczamy odcinki
wyliczamy odcinki 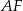 i
i 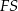 .
.
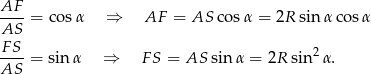
Odcinek 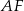 to połowa przekątnej kwadratu w podstawie, więc łatwo wyliczyć długość boku
to połowa przekątnej kwadratu w podstawie, więc łatwo wyliczyć długość boku  tego kwadratu.
tego kwadratu.
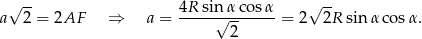
Wysokość 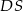 ściany bocznej wyliczamy z trójkąta
ściany bocznej wyliczamy z trójkąta 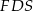
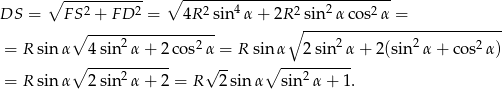
Możemy teraz policzyć pole powierzchni całkowitej.
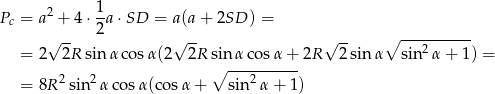
Odpowiedź: