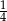Zadanie nr 7239074
Na narysowanej poniżej siatce sześcianu zaznaczono trzy środki ścian sześcianu.
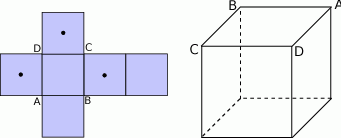
- Zaznacz na powierzchni sześcianu trzy punkty
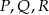odpowiadające środkom ścian wskazanym na jego siatce. - Wiedząc, że krawędź sześcianu ma długość 1, oblicz pole trójkąta
.
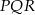Rozwiązanie
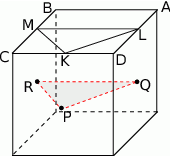
- Łatwo ustalić na których ścianach trzeba postawić kropki – są to ściany sąsiednie do
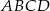i zawierające kolejno krawędzie 
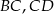i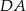 
. 
- Pole trójkąta
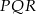łatwo wyliczyć myśląc o odcinku 
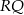jak jego podstawie. Mamy 
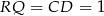. Ponadto wysokość trójkąta 
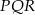opuszczona z wierzchołka 
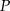ma długość 
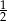(połowa krawędzi sześcianu). Zatem pole jest równe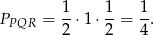 
Jeżeli komuś trudno jest dostrzec co się dzieje, to może sobie patrzeć na trójkąt
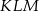, który jest trójkątem 
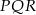przesuniętym na górną ścianę.
Odpowiedź:
