/Szkoła średnia/Geometria/Stereometria

Zadanie nr 7334127

Dodaj do ulubionych
Dodaj do rozwiązanych

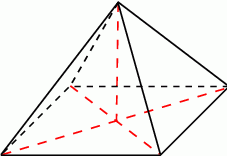
Dany jest ostrosłup prawidłowy czworokątny, w którym wszystkie krawędzie mają równą długość. Zaznacz na rysunku kąt utworzony przez dwie sąsiednie ściany boczne tego ostrosłupa i oblicz cosinus tego kąta.

PIC

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

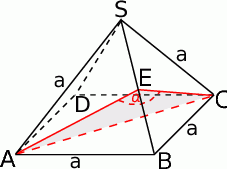
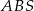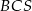Musimy na początek ustalić, jak zaznaczyć interesujący nas kąt między sąsiednimi ścianami bocznymi. Ponieważ trójkąty w ścianach bocznych są równoboczne, gdy opuścimy wysokości w trójkątach ABS i BCS na krawędź 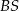BS to przetną one tę krawędź dokładnie w jej środku 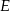E . I mamy to, o co nam chodziło: płaszczyzna 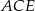ACE jest teraz prostopadła do krawędzi 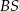BS , zatem interesujący nas kąt, to kąt przy wierzchołku 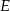E w trójkącie AEC .

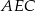Jego cosinus możemy łatwo wyliczyć z twierdzenia cosinusów. Ze wzoru na wysokość w trójkącie równobocznym mamy 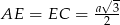a√ 3 AE = EC = -2-- . Ponadto 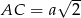√ -- AC = a 2 , więc z twierdzenia cosinusów w trójkącie 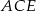ACE mamy

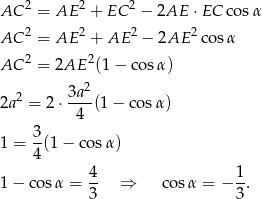
AC 2 = AE 2 + EC 2 − 2AE ⋅ EC cos α 2 2 2 2 AC = AE + AE − 2AE c osα 2 2 AC = 2AE (1 − cos α) 2 3a 2 2a = 2 ⋅-4--(1− cosα ) 3 1 = -(1 − cosα ) 4 4- 1- 1 − cos α = 3 ⇒ cos α = − 3 .

 
Odpowiedź: − 1 3

Wersja PDF