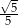/Szkoła średnia/Geometria/Stereometria

Zadanie nr 7651989

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz cosinus kąta między ścianą boczną i płaszczyzną podstawy ostrosłupa prawidłowego trójkątnego, jeżeli wiadomo, że promień okręgu opisanego na podstawie, wysokość ostrosłupa i krawędź boczna tworzą trójkąt równoramienny.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

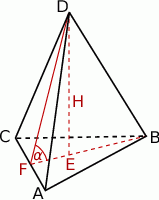
Z treści zadania wiemy, że trójkąt 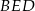BED jest równoramienny, więc jeżeli oznaczymy 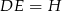DE = H to

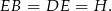
EB = DE = H .

Środek okręgu opisanego na trójkącie równobocznym dzieli odcinek 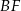BF w stosunku 2:1, więc

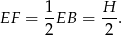
1- H- EF = 2EB = 2 .

To pozwala obliczyć długość odcinka 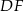DF – patrzymy na trójkąt prostokątny F ED .

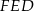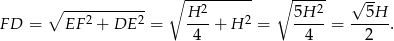
∘ ---------- ∘ ----- √ -- ∘ ----------- H 2 5H 2 5H FD = EF 2 + DE 2 = ---+ H 2 = -----= -----. 4 4 2

Mamy zatem

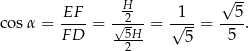
√ -- EF H- 1 5 cos α = ----= √-2--= √---= ---. F D --52H 5 5

 
Odpowiedź: √ - --5 5

Wersja PDF