/Szkoła średnia/Geometria/Stereometria

Zadanie nr 7696300

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą prostopadłościanu jest kwadrat o boku długości 4, a wysokość prostopadłościanu jest równa 8. Połączono odcinkami środki trzech krawędzi prostopadłościanu, które mają wspólny wierzchołek i otrzymano trójkąt 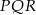P QR

  • Oblicz długości boków trójkąta P QR .
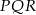  • Wyznacz sinusy kątów trójkąta PQR .

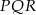Rozwiązanie

  • Zaczynamy oczywiście od rysunku.
    PIC

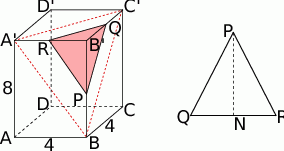
    Ponieważ odcinek łączący środki dwóch boków trójkąta jest dwa razy krótszy od trzeciego boku (twierdzenie Talesa), więc

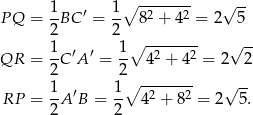
    ∘ ------- -- P Q = 1-BC ′ = 1- 8 2 + 42 = 2√ 5 2 2 1 ′ ′ 1∘ ------- √ -- QR = 2-C A = 2- 42 + 42 = 2 2 ∘ ------- √ -- RP = 1-A′B = 1- 42 + 82 = 2 5. 2 2

     
    Odpowiedź: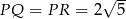 -- PQ = P R = 2√ 5 , √ -- QR = 2 2

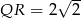
  • Narysujmy sobie z boku trójkąt równoramienny 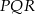P QR . Mamy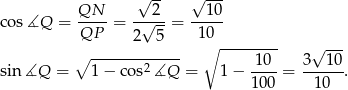
    √ -- √ --- cos ∡Q = QN--= -√-2-= --10- QP 2 5 10 ∘ ------------- ∘ -------- √ --- sin∡Q = 1 − co s2∡Q = 1 − -10-= 3--1-0. 100 10

    Sinus kąta 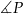∡P możemy wyliczyć z twierdzenia sinusów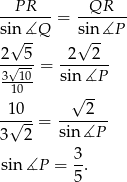

    PR QR ------- = ------- si√n∡Q √sin-∡P 2--5- -2--2-- 3√ 10-= sin ∡P -10-- 10 √ 2- -√---= ------- 3 2 sin∡P 3- sin∡P = 5.

     
    Odpowiedź: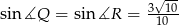 3√ 10 sin∡Q = sin ∡R = -10-- , sin ∡P = 3 5

Wersja PDF