Zadanie nr 7759314
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 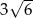 , a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.
, a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.
Rozwiązanie
Zaczynamy oczywiście od rysunku (rysunek tak naprawdę jest trudny do narysowania, bo trójkąty w ścianach bocznych są rozwartokątne, ale jeżeli tego nie zauważmy to nic nie szkodzi – nie ma specjalnego wpływu na obliczenia).
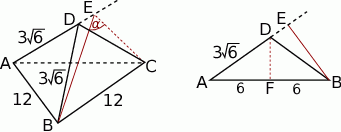
Musimy najpierw ustalić jak wyliczyć kąt między ścianami bocznymi. Ogólnie, taki kąt wyznacza się przecinając kąt dwuścienny płaszczyzną prostopadłą do krawędzi kąta i liczy się miarę otrzymanego kąta płaskiego. W naszej sytuacji sprawa jest dość prosta. Jeżeli poprowadzimy wysokości 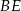 i
i 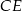 w trójkątach ścian bocznych, opuszczone na krawędź
w trójkątach ścian bocznych, opuszczone na krawędź 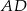 , to ponieważ ostrosłup jest prawidłowy (ściany są przystające), spodki tych wysokości będą dokładnie w tym samym punkcie, oznaczmy go przez
, to ponieważ ostrosłup jest prawidłowy (ściany są przystające), spodki tych wysokości będą dokładnie w tym samym punkcie, oznaczmy go przez 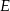 . Otrzymana płaszczyzna
. Otrzymana płaszczyzna 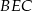 jest prostopadła do krawędzi
jest prostopadła do krawędzi 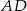 , zatem kąt
, zatem kąt 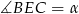 jest kątem między ścianami bocznymi.
jest kątem między ścianami bocznymi.
Cosinus szukanego kąta będziemy mogli wyliczyć z twierdzenia cosinusów w trójkącie 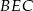 . Aby to zrobić, musimy wyliczyć długości wysokości
. Aby to zrobić, musimy wyliczyć długości wysokości 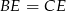 .
.
Narysujmy sobie z boku trójkąt 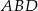 . Chcemy wyliczyć jego wysokość
. Chcemy wyliczyć jego wysokość 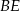 . Wyliczymy najpierw z twierdzenia Pitagorasa wysokość
. Wyliczymy najpierw z twierdzenia Pitagorasa wysokość 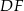
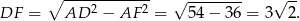
Porównajmy teraz dwa wzory na pole trójkąta 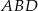 (inny sposób, to podobieństwo trójkątów
(inny sposób, to podobieństwo trójkątów 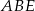 i
i 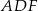 )
)
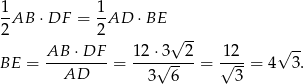
Pozostało zastosować twierdzenie cosinusów do trójkąta 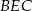 .
.
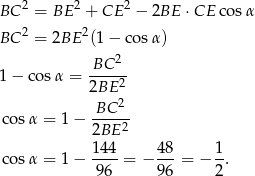
Zatem 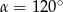 .
.
Odpowiedź: