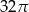/Szkoła średnia/Geometria/Stereometria

Zadanie nr 7948297

Dodaj do ulubionych
Dodaj do rozwiązanych

Kąt rozwarcia stożka jest równy 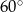∘ 60 . Promień podstawy stożka ma długość 4. Oblicz pole powierzchni bocznej stożka.

Rozwiązanie

Szkicujemy stożek.

PIC

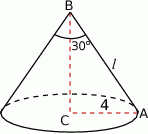
Sposób I

Patrzymy na trójkąt prostokątny 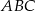ABC .

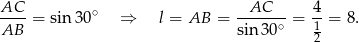
AC--= sin 30∘ ⇒ l = AB = -AC----= 4-= 8. AB sin30∘ 12

Liczymy pole powierzchni bocznej.

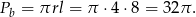
Pb = πrl = π ⋅4⋅ 8 = 32π .

Sposób II

Zauważmy, ze przekrój osiowy stożka jest trójkątem równoramiennym z kątem 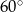60 ∘ . Jest to więc trójkąt równoboczny, czyli 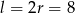l = 2r = 8 . Liczymy pole powierzchni bocznej.

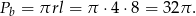
P = πrl = π ⋅4⋅ 8 = 32π . b

 
Odpowiedź: 32π

Wersja PDF