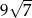Zadanie nr 7951755
Przekątna prostopadłościanu ma długość 5 i tworzy z dwoma ścianami prostopadłościanu kąty  i
i 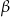 takie, że
takie, że 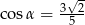 i
i 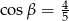 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Rozwiązanie
Zaczynamy oczywiście od rysunku.
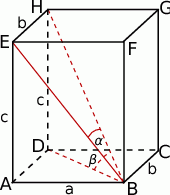
Zauważmy, że przy oznaczeniach z rysunku, z trójkątów prostokątnych 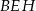 i
i 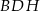 łatwo można wyliczyć długości krawędzi
łatwo można wyliczyć długości krawędzi 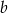 i
i  . Potrzebujemy do tego jednak wartości
. Potrzebujemy do tego jednak wartości 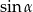 i
i 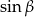 . Zacznijmy od ich wyliczenia
. Zacznijmy od ich wyliczenia
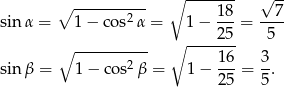
Mamy zatem
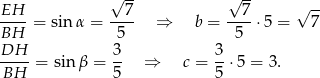
Pozostało wyliczyć długość trzeciej krawędzi prostopadłościanu, zrobimy to korzystając z podanej długości jego przekątnej.
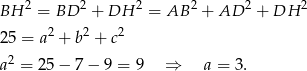
Zatem objętość jest równa
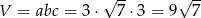
Odpowiedź: