Zadanie nr 7962051
Przekątna 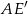 graniastosłupa prawidłowego sześciokątnego ma długość
graniastosłupa prawidłowego sześciokątnego ma długość 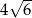 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem 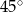 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
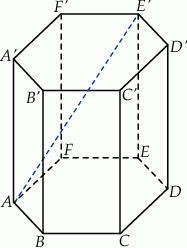
Rozwiązanie
Zaznaczmy na rysunku kąt nachylenia przekątnej i dorysujmy przekątne podstawy.
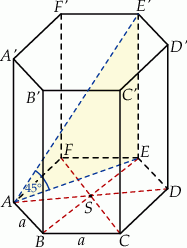
Zauważmy, że trójkąt 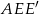 jest prostokątny i równoramienny (bo kąt ostry ma miarę
jest prostokątny i równoramienny (bo kąt ostry ma miarę 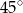 ) – jest to więc połówka kwadratu. Zatem
) – jest to więc połówka kwadratu. Zatem
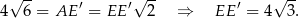
Ponadto 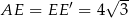 .
.
Zauważmy, że przekątne dzielą sześciokąt w podstawie na 6 trójkątów równobocznych i odcinek 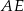 ma długość dwa razy większą od wysokości tych trójkątów. Jeżeli więc oznaczymy przez
ma długość dwa razy większą od wysokości tych trójkątów. Jeżeli więc oznaczymy przez  długość krawędzi podstawy, to
długość krawędzi podstawy, to
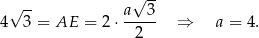
Pozostało obliczyć objętość
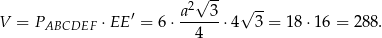
Odpowiedź: 288

