Zadanie nr 8086417
Wykaż, że objętość sześcianu jest sześć razy większa od objętości ośmiościanu foremnego, wyznaczonego przez środki ścian tego sześcianu.
Rozwiązanie
Szkicujemy opisaną sytuację – oznaczmy krawędź sześcianu przez 
.
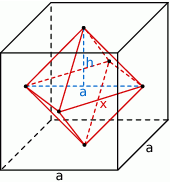
Gdy się przyjrzymy to widać, że ośmiościan wpisany w sześcian składa się z dwóch ostrosłupów prawidłowych czworokątnych, których podstawa jest kwadratem o przekątnej długości 
, i których wysokość ma długość 
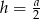. W takim razie jeżeli oznaczmy długość krawędzi ośmiościanu przez 
to mamy
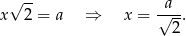
Objętość ośmiościanu jest więc równa
