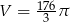Zadanie nr 8099890
Trójkąt o bokach długości 5, 8 i 9 obraca się dookoła najdłuższego boku. Oblicz objętość powstałej bryły.
Rozwiązanie
Zaczynamy oczywiście od rysunku.
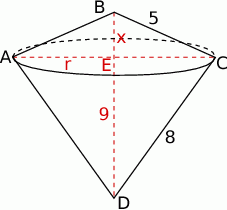
Otrzymana bryła składa się z dwóch stożków o wspólnej podstawie. Aby obliczyć ich objętości musimy wyznaczyć długość  promienia tej podstawy. Zrobimy to na dwa sposoby.
promienia tej podstawy. Zrobimy to na dwa sposoby.
Sposób I
Jeżeli oznaczymy 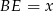 , to obliczając długość odcinka
, to obliczając długość odcinka 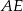 z twierdzenia Pitagorasa w trójkątach
z twierdzenia Pitagorasa w trójkątach 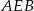 i
i 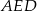 mamy równanie
mamy równanie
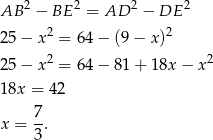
Stąd
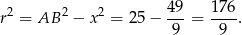
Stąd szukana objętość wynosi
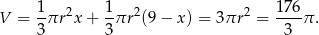
Sposób II
Długość promienia  to dokładnie wysokość opuszczona na bok
to dokładnie wysokość opuszczona na bok 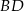 w trójkącie
w trójkącie 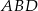 . Aby ją wyznaczyć wystarczy znać pole trójkąta, a to możemy obliczyć ze wzoru Herona. Mamy
. Aby ją wyznaczyć wystarczy znać pole trójkąta, a to możemy obliczyć ze wzoru Herona. Mamy 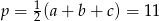 oraz
oraz
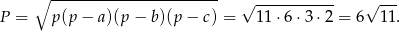
Stąd
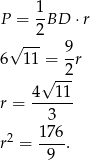
Dalej liczymy jak w poprzednim sposobie.
Odpowiedź: