Zadanie nr 8104953
Trapez prostokątny obraca się wokół boku tworzącego z podstawami kąty proste. Podstawy trapezu mają długość odpowiednio 10 cm i 7 cm. Pole trapezu wynosi 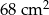 . Oblicz objętość otrzymanej bryły.
. Oblicz objętość otrzymanej bryły.
Rozwiązanie
Rysujemy najpierw rysunek.
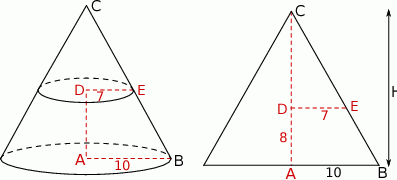
Bryła którą otrzymamy to ścięty stożek, którego promienie wynoszą 7 i 10 odpowiednio. Jego wysokość to dokładnie wysokość trapezu, możemy więc ją obliczyć z podanego pola.
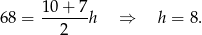
Objętość tego stożka to różnica objętości ’dużego’ stożka o wysokości 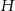 i promieniu podstawy 10 oraz mniejszego o wysokości
i promieniu podstawy 10 oraz mniejszego o wysokości 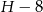 i promieniu podstawy 7. Aby wyliczyć
i promieniu podstawy 7. Aby wyliczyć 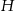 popatrzmy na przekrój osiowy otrzymanej figury. Z podobieństwa trójkątów
popatrzmy na przekrój osiowy otrzymanej figury. Z podobieństwa trójkątów 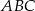 i
i 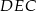 mamy
mamy
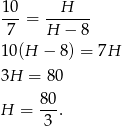
Liczymy teraz szukaną objętość
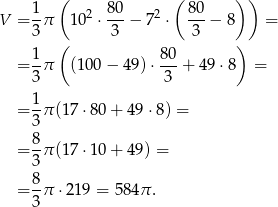
Odpowiedź: