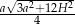/Szkoła średnia/Geometria/Stereometria

Zadanie nr 8130842

Dodaj do ulubionych
Dodaj do rozwiązanych

Wysokość prawidłowego ostrosłupa sześciokątnego ma długość 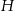H , a krawędź podstawy ma długość a . Wyznacz pole przekroju wyznaczonego przez krótszą przekątną podstawy i wierzchołek ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku.

PIC

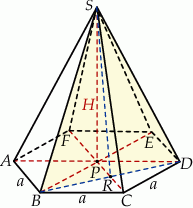
Jeżeli połączymy w podstawie przeciwległe wierzchołki, to otrzymamy 6 trójkątów równobocznych o boku a . Podstawa 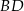BD interesującego nas przekroju ma długość dwóch wysokości tych trójkątów równobocznych, czyli

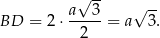
-- a √ 3 √ -- BD = 2 ⋅----- = a 3. 2

Wysokość SR przekroju obliczymy z trójkąta prostokątnego P RS

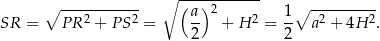
∘ ----------- ∘ (--)-2------ ∘ --------- SR = P R2 + P S2 = a- + H 2 = 1- a2 + 4H 2. 2 2

Zatem pole przekroju jest równe

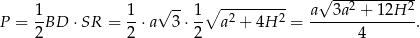
√ -- ∘ --------- √ --2-------2- P = 1BD ⋅SR = 1⋅ a 3⋅ 1- a 2 + 4H 2 = a--3a--+-12H--. 2 2 2 4

 
Odpowiedź: √ -2-----2 a--3a+4-12H--

Wersja PDF