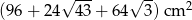/Szkoła średnia/Geometria/Stereometria

Zadanie nr 8265296

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa jest prostokąt o polu 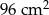2 96 cm kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 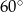6 0∘ . Oblicz pole powierzchni całkowitej tej bryły.

Rozwiązanie

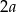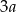Zacznijmy od wyliczenia długości boków prostokąta w podstawie. Jeżeli oznaczymy ich długości przez 2a i 3a , to mamy równanie

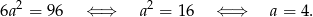
6a2 = 96 ⇐ ⇒ a2 = 16 ⇐ ⇒ a = 4.

Zatem boki prostokąta mają długości 8 i 12.

Teraz narysujmy sobie ostrosłup.

PIC

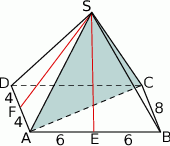
Ponieważ wszystkie krawędzie są nachylone do podstawy pod kątem 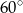60∘ , trójkąt 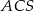ACS jest równoboczny. Długość jego boku wynosi

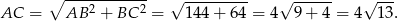
∘ ------------ √ --------- √ ------ √ --- AC = AB 2 + BC 2 = 144 + 64 = 4 9+ 4 = 4 13 .

Ściany ostrosłupa są trójkątami równoramiennymi i ich wysokości wynoszą

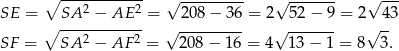
∘ ------------ √ --------- √ ------- √ --- SE = SA 2 − AE 2 = 2 08− 36 = 2 52 − 9 = 2 43 ∘ ------------ √ --------- √ ------- √ -- SF = SA 2 − AF 2 = 20 8− 16 = 4 13 − 1 = 8 3.

Liczymy teraz pole powierzchni.

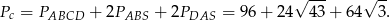
√ --- √ -- P = P + 2P + 2P = 96 + 24 43+ 64 3. c ABCD ABS DAS

 
Odpowiedź: √ --- √ -- 2 (96 + 24 43+ 64 3) cm

Wersja PDF