Zadanie nr 8366202
Podstawa stożka o kącie rozwarcia 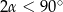 jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu
jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu  .
.
Rozwiązanie
Zacznijmy od narysowania przekroju osiowego opisanej sytuacji.
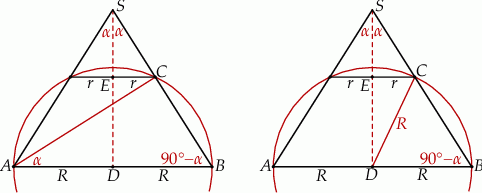
Sposób I
Z trójkąta prostokątnego 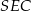 mamy
mamy
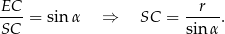
Ponieważ 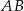 jest średnicą okręgu będącego przekrojem kuli, trójkąty
jest średnicą okręgu będącego przekrojem kuli, trójkąty 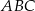 i
i 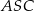 są prostokątne. W trójkącie prostokątnym
są prostokątne. W trójkącie prostokątnym 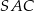 mamy
mamy
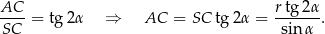
Teraz patrzymy na trójkąt prostokątny 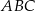 .
.
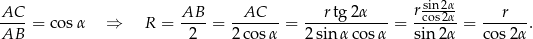
Teraz patrzymy na trójkąt prostokątny 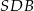 .
.
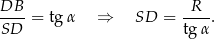
Objętość stożka jest więc równa
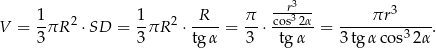
Sposób II
Tym razem połączmy środek 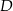 kuli z punktem
kuli z punktem 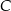 . Trójkąt
. Trójkąt 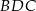 jest równoramienny, więc
jest równoramienny, więc
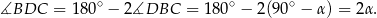
Stąd
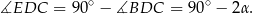
Patrzymy teraz na trójkąt prostokątny 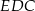 .
.
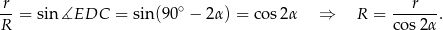
Wysokość i objętość ostrosłupa obliczamy dokładnie tak samo jak w poprzednim sposobie.
Odpowiedź: