/Szkoła średnia/Geometria/Stereometria

Zadanie nr 8447505

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz objętość i pole powierzchni bocznej ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy 2 cm i krawędzi bocznej 6 cm.

Rozwiązanie

Zaczynamy od rysunku.

PIC

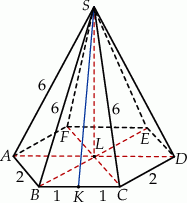
Jeżeli połączymy środek sześciokąta w podstawie z jego wierzchołkami, to otrzymamy 6 trójkątów równobocznych. Możemy więc łatwo obliczyć wysokość ostrosłupa z trójkąta prostokątnego 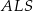ALS .

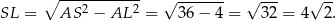
∘ ------------ √ ------- √ --- √ -- SL = AS 2 − AL 2 = 36 − 4 = 32 = 4 2 .

Zatem objętość jest równa (korzystamy ze wzoru na pole trójkąta równobocznego).

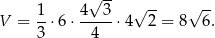
1 4√ 3- √ -- √ -- V = --⋅6 ⋅-----⋅4 2 = 8 6. 3 4

Aby obliczyć pole powierzchni bocznej, obliczamy najpierw (z trójkąta prostokątnego 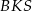BKS ) wysokość ściany bocznej

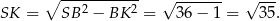
∘ ----------- √ ------- √ --- SK = SB 2 − BK 2 = 36 − 1 = 3 5.

Zatem pole powierzchni bocznej jest równe

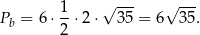
1 √ --- √ --- Pb = 6⋅ -⋅2 ⋅ 35 = 6 35. 2

 
Odpowiedź: 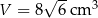√ -- V = 8 6 cm 3 , √ --- Pb = 6 35 cm 2

Wersja PDF