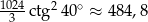/Szkoła średnia/Geometria/Stereometria

Zadanie nr 8602961

Dodaj do ulubionych
Dodaj do rozwiązanych

Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 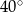40 ∘ . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

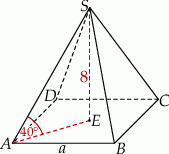
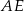Jeżeli oznaczymy długość krawędzi podstawy ostrosłupa przez a to odcinek AE ma długość równą połowie długości przekątnej kwadratu 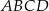ABCD , czyli 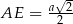a√2- AE = 2 . Z trójkąta prostokątnego 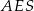AES mamy

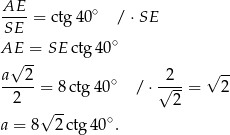
AE ∘ ---- = ctg 40 / ⋅SE SE ∘ AE = SE ctg40 a √ 2- 2 √ -- ----- = 8 ctg 40∘ / ⋅√---= 2 2 √ -- 2 a = 8 2ctg 40∘.

Zatem objętość ostrosłupa jest równa

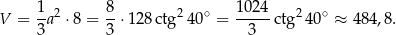
1 2 8 2 ∘ 10 24 2 ∘ V = -a ⋅8 = --⋅12 8ctg 4 0 = -----ctg 40 ≈ 48 4,8. 3 3 3

 
Odpowiedź: 1024 2 ∘ 3 ctg 40 ≈ 4 84,8

Wersja PDF