Zadanie nr 8628592
W prostopadłościanie poprowadzono z jednego wierzchołka przekątne ścian bocznych, obie o długości 4. Wiedząc, że kąt między tymi przekątnymi ma miarę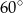 
, oblicz pole powierzchni tego prostopadłościanu.
Rozwiązanie
Rozpoczynamy od rysunku.
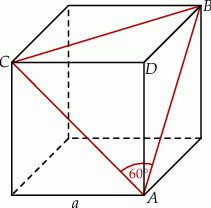
Powiedzmy, że przekątne, o których mowa to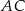 
i 
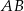. W takim razie trójkąt 
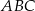jest równoramienny i kąt między ramionami wynosi 
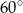. Musi to więc być trójkąt równoboczny (bo pozostałe kąty też muszą mieć po 
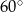), czyli 
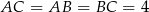. To oznacza, że trójkąty 
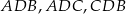są przystające (bo są prostokątne i każde dwa mają dwa równe boki). Zatem dany prostopadłościan to sześcian. Jeżeli oznaczymy długość jego krawędzi przez 
to ze wzoru na przekątną kwadratu mamy
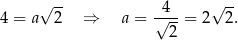
Jego pole powierzchni jest równe
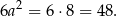
Odpowiedź: 48
