/Szkoła średnia/Geometria/Stereometria

Zadanie nr 8736473

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą ostrosłupa 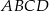ABCD jest trójkąt 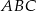ABC . Krawędź 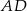AD jest wysokością ostrosłupa (zobacz rysunek).

PIC

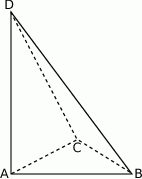
Oblicz objętość ostrosłupa 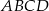ABCD , jeśli wiadomo, że 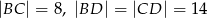|BC | = 8, |BD | = |CD | = 14 oraz pole podstawy jest równe 24.

Rozwiązanie

Podpiszmy długości krawędzi.

PIC

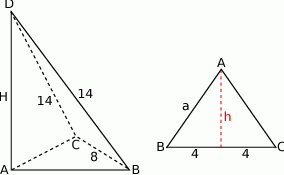
Zauważmy, że

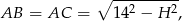
∘ --------- AB = AC = 142 − H 2,

czyli trójkąt 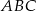ABC jest równoramienny. Znamy ponadto jego pole, więc łatwo wyliczyć długość jego wysokości 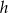h opuszczonej na bok BC .

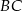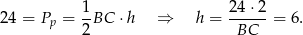
24 = P = 1-BC ⋅ h ⇒ h = 24⋅2-= 6. p 2 BC

Stąd

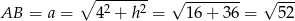
∘ -------- √ -------- √ --- AB = a = 42 + h2 = 16 + 36 = 52

oraz z trójkąta ABD

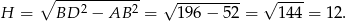
∘ ------------ √ --------- √ ---- H = BD 2 − AB 2 = 1 96− 52 = 144 = 12.

Zatem objętość ostrosłupa jest równa

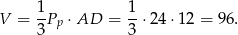
V = 1Pp ⋅AD = 1-⋅24 ⋅12 = 96. 3 3

 
Odpowiedź: 96

Wersja PDF