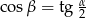Zadanie nr 8765577
Graniastosłup prawidłowy czworokątny przecięto płaszczyzną, przechodzącą przez jeden punkt z wierzchołków podstawy, otrzymując w przekroju romb o kącie ostrym  . Wyznacz
. Wyznacz 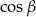 , gdzie
, gdzie 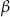 jest kątem nachylenia płaszczyzny przekroju do płaszczyzny podstawy bryły.
jest kątem nachylenia płaszczyzny przekroju do płaszczyzny podstawy bryły.
Rozwiązanie
Zaczynamy oczywiście od rysunku. Graniastosłup prawidłowy czworokątny to po prostu prostopadłościan, którego podstawą jest kwadrat – oznaczmy jego bok przez  .
.
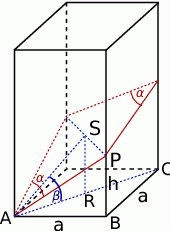
Aby wyliczyć 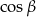 potrzebujemy wyliczyć długości odcinków
potrzebujemy wyliczyć długości odcinków 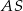 i
i 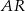 . Ten drugi to po prostu
. Ten drugi to po prostu 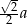 (połowa przekątnej kwadratu), zajmijmy się więc wyliczeniem
(połowa przekątnej kwadratu), zajmijmy się więc wyliczeniem 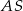 . Zauważmy, że
. Zauważmy, że 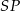 jest również połową przekątnej kwadratu, więc z trójkąta prostokątnego
jest również połową przekątnej kwadratu, więc z trójkąta prostokątnego 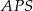 mamy
mamy
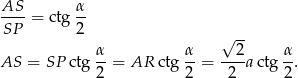
Mamy zatem
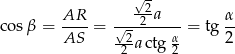
Oczywiście, jak już wiemy co ma wyjść, to całe te rachunki mogliśmy zapisać prościej
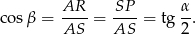
Odpowiedź: