Zadanie nr 8811814
W ostrosłupie prawidłowym trójkątnym 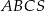 krawędź podstawy ma długość 12, a jego objętość jest równa
krawędź podstawy ma długość 12, a jego objętość jest równa 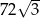 . Kąt
. Kąt  jest kątem między krawędziami bocznymi
jest kątem między krawędziami bocznymi 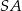 i
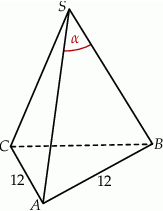
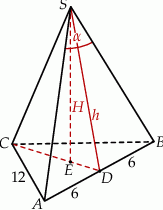
i 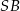 (zobacz rysunek). Oblicz sinus kąta
(zobacz rysunek). Oblicz sinus kąta  .
.
Rozwiązanie
Dorysujmy wysokość 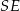 ostrosłupa oraz wysokość
ostrosłupa oraz wysokość 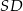 jego ściany bocznej
jego ściany bocznej  .
.
Z podanej objętości możemy obliczyć wysokość 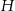 ostrosłupa (korzystamy ze wzoru:
ostrosłupa (korzystamy ze wzoru: 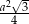 na pole trójkąta równobocznego o boku
na pole trójkąta równobocznego o boku  ).
).
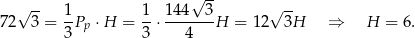
Teraz z trójkąta prostokątnego 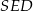 obliczamy wysokość
obliczamy wysokość 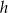 ściany bocznej.
ściany bocznej.
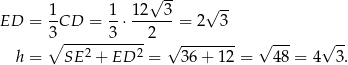
Obliczmy jeszcze długość krawędzi bocznej – korzystamy z trójkąta prostokątnego 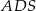 .
.
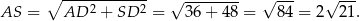
Interesujący nas 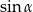 obliczymy na dwa sposoby.
obliczymy na dwa sposoby.
Sposób I
Korzystamy ze wzoru na pole trójkąta z sinusem.
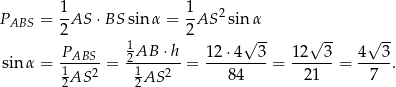
Sposób II
Korzystamy ze wzoru
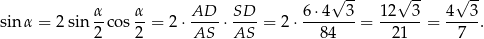
Odpowiedź: