Zadanie nr 8817781
Drewnianą kulę o promieniu 5 cm pocięto na 5 części w ten sposób, że płaszczyzny cięcia są prostopadłe do ustalonej średnicy 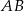 tej kuli, oraz podzieliły tę średnicę na 5 równych odcinków. Oblicz pola powierzchni otrzymanych przekrojów kołowych.
tej kuli, oraz podzieliły tę średnicę na 5 równych odcinków. Oblicz pola powierzchni otrzymanych przekrojów kołowych.
Rozwiązanie
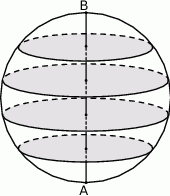
Narysujmy przekrój osiowy opisanej sytuacji.
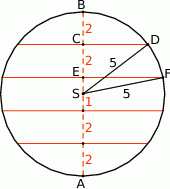
Ponieważ średnica kuli ma długość 10, płaszczyzny cięcia podzieliły średnicę na odcinki długości 2.
Widać, że otrzymaliśmy cztery przekroje, przy czym dwa dolne mają takie same pole jak dwa górne. Każdy przekrój jest kołem, więc zadanie sprowadza się do wyznaczenia promieni tych kół.
Zacznijmy od najwyższego przekroju. Z trójkąta prostokątnego 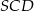 mamy
mamy
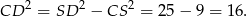
Pole tego przekroju jest więc równe
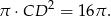
Obliczmy teraz promień większego przekroju.
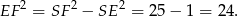
Pole większego przekroju jest więc równe
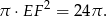
Odpowiedź: