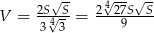/Szkoła średnia/Geometria/Stereometria

Zadanie nr 8920280

Dodaj do ulubionych
Dodaj do rozwiązanych

Przekrój ostrosłupa prawidłowego czworokątnego zawierającego przekątną podstawy oraz wierzchołek ostrosłupa jest trójkątem równobocznym o polu 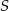S . Oblicz objętość tego ostrosłupa . Wykonaj rysunek pomocniczy.

Rozwiązanie

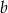Oznaczmy przez a długość krawędzi podstawy, a przez b długość krawędzi bocznej ostrosłupa.

PIC

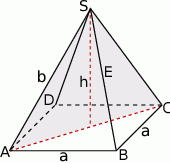
Z wzoru na pole trójkąta równobocznego mamy

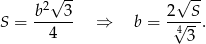
2√ -- √ -- S = b---3- ⇒ b = 2√--S. 4 43

Wiemy również, że przekątna podstawy ma długość 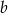b , więc

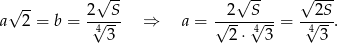
√ -- √ -- √ --- √ -- 2 S 2 S 2S a 2 = b = √4--- ⇒ a = √----√4--= -4√---. 3 2 ⋅ 3 3

Ze wzoru na wysokość w trójkącie równobocznym obliczamy wysokość 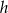h ostrosłupa.

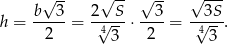
√ -- √ -- √ -- √ --- h = b--3-= 2√-S-⋅---3 = -√3S-. 2 4 3 2 43

Pozostało obliczyć objętość ostrosłupa

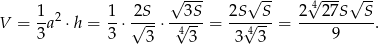
√ --- √ -- √ --- √ -- 1- 2 1- 2S-- --3S- 2S---S 2-427S---S- V = 3 a ⋅h = 3 ⋅√ --⋅ √4-- = √4-- = 9 . 3 3 3 3

 
Odpowiedź: 2S√S- 2√427S√S V = 34√3 = 9

Wersja PDF