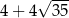/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9121556

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

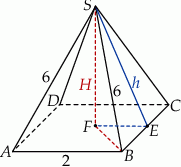
Wysokość 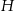H ostrosłupa wyliczamy z trójkąta prostokątnego 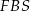FBS . Odcinek 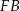F B ma długość połowy przekątnej kwadratu w podstawie, czyli 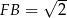√ -- FB = 2 . Mamy więc

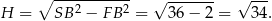
∘ ----------- H = SB 2 − F B2 = √ 3-6−-2-= √ 34.

Zatem objętość ostrosłupa jest równa

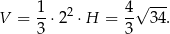
1- 2 4-√ --- V = 3 ⋅2 ⋅H = 3 34.

Aby obliczyć pole powierzchni ostrosłupa musimy znać długość 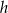h wysokości ściany bocznej. Wyliczamy ją z trójkąta prostokątnego F ES .

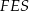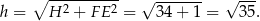
---------- ∘ 2 2 √ ------- √ --- h = H + FE = 34+ 1 = 35.

Zatem pole powierzchni ostrosłupa jest równe

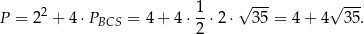
2 1 √ --- √ --- P = 2 + 4 ⋅PBCS = 4 + 4 ⋅2-⋅2⋅ 35 = 4 + 4 35 .

 
Odpowiedź: Objętość: 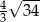4√ --- 3 34 , pole powierzchni: √ --- 4 + 4 35

Wersja PDF