/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9131991

Dodaj do ulubionych
Dodaj do rozwiązanych

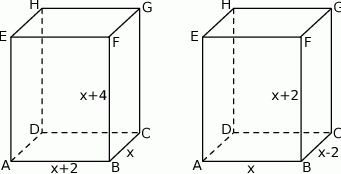
Długości trzech krawędzi wychodzących z jednego wierzchołka prostopadłościanu są kolejnymi liczbami nieparzystymi. Pole powierzchni całkowitej prostopadłościanu wynosi 142. Oblicz objętość tego prostopadłościanu.

Rozwiązanie

Sposób I

Oznaczmy długości krawędzi prostopadłościanu przez 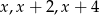x,x + 2,x + 4 .

PIC

Z podanej informacji o polu powierzchni całkowitej mamy równanie

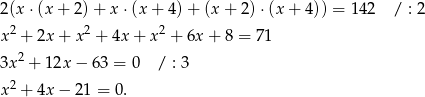
2(x ⋅(x + 2) + x ⋅(x+ 4)+ (x+ 2)⋅(x + 4)) = 142 / : 2 2 2 2 x + 2x + x + 4x + x + 6x + 8 = 71 3x2 + 12x − 6 3 = 0 / : 3 2 x + 4x − 21 = 0.

Rozwiązujemy otrzymane równanie kwadratowe

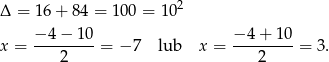
2 Δ = 16 + 84 = 100 = 1 0 −-4-−-10- −-4-+-10- x = 2 = − 7 lub x = 2 = 3.

Ujemne rozwiązanie odrzucamy i krawędzie prostopadłościanu mają długości: 3, 5, 7. Obliczamy jego objętość.

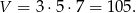
V = 3⋅5 ⋅7 = 10 5.

Sposób II

Tym razem oznaczmy długości krawędzi prostopadłościanu przez 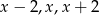x − 2,x,x + 2 . Z podanej informacji o polu powierzchni całkowitej mamy równanie

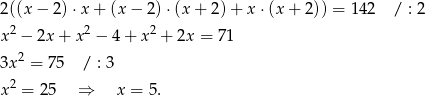
2((x − 2) ⋅x + (x − 2)⋅ (x+ 2)+ x⋅(x + 2)) = 142 / : 2 2 2 2 x − 2x + x − 4 + x + 2x = 71 3x2 = 7 5 / : 3 2 x = 25 ⇒ x = 5.

Objętość prostopadłościanu jest więc równa.

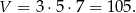
V = 3⋅5 ⋅7 = 10 5.

 
Odpowiedź: 105

Wersja PDF