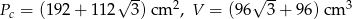/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9142761

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 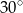30∘ . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.

Rozwiązanie

Zaczynamy od rysunku.

PIC

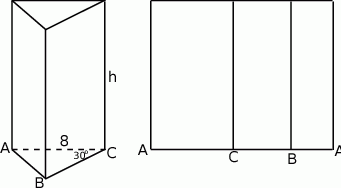
Policzmy przyprostokątne trójkąta w podstawie.

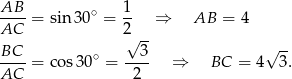
AB--= sin30 ∘ = 1- ⇒ AB = 4 AC 2√ -- BC ∘ 3 √ -- ----= cos 30 = ---- ⇒ BC = 4 3. AC 2

Z podanej informacji o rozwinięciu powierzchni bocznej wynika, że

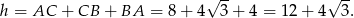
h = AC + CB + BA = 8+ 4√ 3+ 4 = 12 + 4√ 3-.

Liczmy pole powierzchni całkowitej i objętość

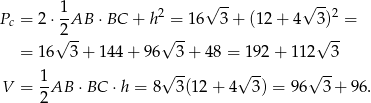
1- 2 √ -- √ --2 Pc = 2⋅ 2AB ⋅BC + h = 16 3+ (12+ 4 3) = √ -- √ -- √ -- = 16 3 + 144 + 96 3+ 48 = 192 + 11 2 3 1- √ -- √ -- √ -- V = 2AB ⋅BC ⋅h = 8 3(12+ 4 3) = 96 3+ 96.

 
Odpowiedź: P = (19 2+ 1 12√ 3) cm 2, V = (96√ 3-+ 9 6) cm 3 c

Wersja PDF