/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9148330

Dodaj do ulubionych
Dodaj do rozwiązanych

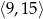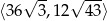Dany jest prostopadłościan o polu powierzchni równym 162, w którym przekątna jest liczbą z przedziału ⟨9,15⟩ . Wykaż, że suma długości wszystkich krawędzi tego prostopadłościanu jest liczbą z przedziału ⟨36 √ 3,12√ 43⟩ .

Rozwiązanie

Szkicujemy prostopadłościan.

PIC

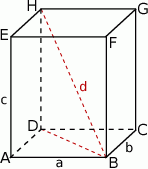
Z podanego pola powierzchni mamy

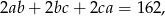
2ab+ 2bc + 2ca = 16 2,

a z podanej długości przekątnej

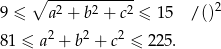
∘ ------------ 9 ≤ a 2 + b2 + c2 ≤ 15 /()2 2 2 2 81 ≤ a + b + c ≤ 225.

Przekształcamy teraz tezę, którą mamy udowodnić, w sposób równoważny.

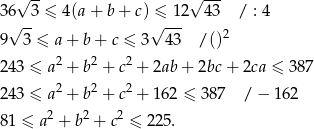
√ -- √ --- 3 6√ -3 ≤ 4(a + b + c)√≤-12 4 3 / : 4 9 3 ≤ a+ b+ c ≤ 3 43 /()2 2 43 ≤ a2 + b2 + c2 + 2ab + 2bc+ 2ca ≤ 387 2 2 2 2 43 ≤ a + b + c + 1 62 ≤ 387 / − 162 8 1 ≤ a2 + b2 + c2 ≤ 225.

Otrzymana nierówność z założenia jest prawdziwa, więc nierówność od której zaczęliśmy przekształcenia też musiała być prawdziwa (bo przekształcaliśmy ją w sposób równoważny).

Wersja PDF