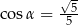/Szkoła średnia/Geometria/Stereometria

Zadanie nr 9156752

Dodaj do ulubionych
Dodaj do rozwiązanych

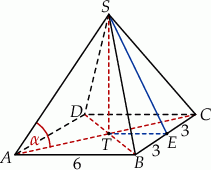
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego jest równa 6. Pole powierzchni całkowitej tego ostrosłupa jest cztery razy większe od pola jego podstawy. Kąt α jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta α .

PIC

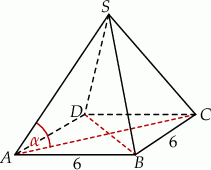
Rozwiązanie

Dorysujmy wysokość 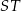ST ostrosłupa oraz wysokość 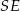SE jego ściany bocznej.

PIC

Wiemy, że pole powierzchni całkowitej ostrosłupa jest równe

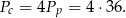
Pc = 4Pp = 4 ⋅36.

Z drugiej strony,

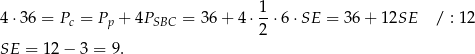
4 ⋅36 = P = P + 4P = 36 + 4 ⋅ 1-⋅6⋅ SE = 36+ 12SE / : 1 2 c p SBC 2 SE = 12 − 3 = 9.

Stosujemy teraz twierdzenie Pitagorasa w trójkącie 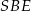SBE i obliczamy długość krawędzi bocznej ostrosłupa.

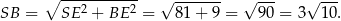
∘ ----------- √ ------- √ --- √ --- SB = SE 2 + BE 2 = 81+ 9 = 90 = 3 10.

Z trójkąta prostokątnego AT S obliczamy interesujący nas cosinus.

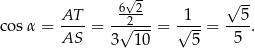
√- √ -- AT 6-2- 1 5 co sα = ----= -√2---= √---= ---. AS 3 10 5 5

 
Odpowiedź: √- cosα = -55-

Wersja PDF